NumPy学习笔记 - Cyrus' Blog

NumPy是一个广泛使用的Python库，NumPy是Numerical Python的缩写，用于多维数组的计算，并且支持对多维数组进行各种数学处理，同时保持非常高的性能。Pandas, SciPy, Matplotlib, scikit-learn等一系列库都使用了NumPy提供的多维数组。

安装#

1
conda install numpy # 如果你使用Anaconda
2
micromamba install numpy # 如果你使用micromamba
3
pip install numpy # 如果你使用pip

引入NumPy#

1
import numpy as np

将NumPy重命名为np不仅能让代码简短，还是一种约定俗成的写法，建议任何时候都这么写。

NumPy中的数组和Python原生的list有什么区别？#

不同点	NumPy array	Python list
元素类型	数组的所有元素必须拥有相同类型	数组的元素可以有不同的类型
内存占有	内存占用少	有额外的内存占用
性能表现	速度快	速度较慢

数组#

数组是NumPy的核心。在NumPy中，数组被称作ndarray，是多维数组（N-Dimensional Array）的缩写。向量（vector）就是1维数组（对于NumPy中的ndarray，向量就是向量，不区分行向量和列向量），矩阵（matrix）就是二维数组，三维以上的数组通常叫做“张量”（tensor）。

创建数组#

创建数组使用的函数有：np.array()、np.zeros()、np.ones()、np.empty()、np.arange、np.linspace()、np.random.rand()。

np.array()接受Python list，返回一个NumPy的ndarray。

1
>>> import numpy as np
2
>>> import numpy as np
3
>>> np.array([1, 2, 3]) # 创建1维数组
4
array([1, 2, 3])
5
>>> np.array([[1, 2, 3], [4, 5, 6]]) # 创建2维数组
6
array([[1, 2, 3],
7
       [4, 5, 6]])
8
>>> np.array([[[1, 2], [3, 4]], [[5, 6], [7, 8]]]) # 创建3维数组
9
array([[[1, 2],
10
        [3, 4]],
11

12
       [[5, 6],
13
        [7, 8]]])
14
>>>

np.zeros()返回全部为0的数组，np.ones()返回全部为1的数组。

1
>>> np.zeros(3)
2
array([0., 0., 0.])
3
>>> np.ones(4)
4
array([1., 1., 1., 1.])
5
>>> np.ones((2, 2)) # 注意生成多维数组要传入元组，而不是多个参数
6
array([[1., 1.],
7
       [1., 1.]])

np.empty()返回一个包含垃圾值的数组，它里面的值是未初始化的随机值。

为什么要使用np.empty()而不是np.zeros()？因为省去了初始化的时间，所以速度更快。如果你需要一个数组来装某些东西，就创建一个np.empty()代表“里面的值之后再确定”。

1
>>> np.empty(2) # 你的输出会和我不一样，这是正常的
2
array([-4.85269502e+281,  1.75993746e-270])

np.arange()就相当于NumPy版本的range()

1
>>> np.arange(5)
2
array([0, 1, 2, 3, 4])
3
>>> np.arange(3, 6)
4
array([3, 4, 5])
5
>>> np.arange(3, 12, 2)
6
array([ 3,  5,  7,  9, 11])

TIP
看不懂？复习一下Python中的range()

np.linspace是用来在两个点之间均匀地取n个点的（包含头尾）

1
>>> np.linspace(0, 10, num = 5)
2
array([ 0. ,  2.5,  5. ,  7.5, 10. ])

np.random.rand()可以生成一个随机的数组

1
>>> np.random.rand(3) # 生成长度为3的一维数组
2
array([0.64400357, 0.61173257, 0.74255108])
3
>>> np.random.rand(2, 3) # 生成2x3的随机数组
4
array([[0.64385017, 0.01831495, 0.20365181],
5
       [0.8246319 , 0.28612528, 0.72145898]])

最后，还有一个可选择的参数dtype需要知道。dtype是用来指定数组里面的元素的类型，如果不指定，默认值为np.float64，大部分创建数组的函数都支持dtype参数。

1
>>> np.ones(3, dtype=np.int64)
2
array([1, 1, 1], dtype=int64)
3
>>> np.arange(1, 11, 2, dtype = np.uint32)
4
array([1, 3, 5, 7, 9], dtype=uint32)
5
>>> np.array([[1, 2], [3, 4]], dtype=complex)
6
array([[1.+0.j, 2.+0.j],
7
       [3.+0.j, 4.+0.j]])

NumPy支持的所有数据类型列表

索引、切片和迭代数组#

在NumPy中，有很多种方式可以索引（indexing）、切片（slicing）和迭代（iterating）数组

1维数组#

1维数组的索引、切片和迭代与原生的list完全相同。

1
>>> arr = np.arange(10)
2
>>> arr[3] # 下标从0开始
3
3
4
>>> arr[-2] # 支持负数倒序访问
5
8
6
>>> arr[3:7] # 切片
7
array([3, 4, 5, 6])
8
>>> arr[2:6:2] # 和Python的语法一致
9
array([2, 4])
10
>>> arr[::-1] # 翻转一个数组
11
array([9, 8, 7, 6, 5, 4, 3, 2, 1, 0])
12
>>> for i in arr: # 迭代也是一样的
13
...     print(i*i, end=' ')
14
...
15
0 1 4 9 16 25 36 49 64 81

TIP
不熟悉？复习Python列表

多维数组#

1
>>> arr = np.arange(1, 26).reshape(5, 5)
2
>>> arr
3
array([[ 1,  2,  3,  4,  5],
4
       [ 6,  7,  8,  9, 10],
5
       [11, 12, 13, 14, 15],
6
       [16, 17, 18, 19, 20],
7
       [21, 22, 23, 24, 25]])
8
>>> arr[2, 3] # 单元素访问，注意从0开始
9
14
10
>>> arr[2:4, 1] # 对第一维切片
11
array([12, 17])
12
>>> arr[2:4, 0:3] # 对两个维度切片
13
array([[11, 12, 13],
14
       [16, 17, 18]])
15
>>> arr[:, 2] # 取第三列
16
array([ 3,  8, 13, 18, 23])
17
>>> arr[4, :] # 取第五行
18
array([21, 22, 23, 24, 25])
19
>>> arr[4] # 和上一个一样，如果后面都是“:”，可以全部省略
20
array([21, 22, 23, 24, 25])
21
>>> arr[-1] # 也可以用负数倒序访问， 效果和上一个一样
22
array([21, 22, 23, 24, 25])
23
>>> arr[:, -1] # 最后一列
24
array([ 5, 10, 15, 20, 25])

...（三个点）可以省略多维数组索引中的多个“:”

1
>>> arr = np.arange(16).reshape(2, 2, 2, 2) # 这是一个4维数组，每一维大小都是2
2
>>> arr
3
array([[[[ 0,  1],
4
         [ 2,  3]],
5

6
        [[ 4,  5],
7
         [ 6,  7]]],
8

9

10
       [[[ 8,  9],
11
         [10, 11]],
12

13
        [[12, 13],
14
         [14, 15]]]])
15
>>> arr[0, ..., 1] # 相当于 arr[0, :, :, 1]
16
array([[1, 3],
17
       [5, 7]])
18
>>> arr[..., 1] # 相当于 arr[:, :, :, 1]
19
array([[[ 1,  3],
20
        [ 5,  7]],
21

22
       [[ 9, 11],
23
        [13, 15]]])

迭代数组时迭代的是他的每一行，如果想要迭代每一个元素，请使用arr.flat（注意没有括号）。

1
>>> arr = np.array([[1, 2], [3, 4]])
2
>>> for i in arr:
3
...     print(i)
4
...
5
[1 2]
6
[3 4]
7
>>> for i in arr.flat():
8
...     print(i)
9
...
10
>>> for i in arr.flat:
11
...     print(i)
12
...
13
1
14
2
15
3
16
4

排序数组#

1
>>> arr = np.array([3, 6, 4, 2, 5, 1])
2
>>> np.sort(arr)
3
array([1, 2, 3, 4, 5, 6])

拼接数组#

1
>>> arr1 = np.array([3, 4, 5])
2
>>> arr2 = np.ones(4)
3
>>> np.concatenate((arr1, arr2))
4
array([3., 4., 5., 1., 1., 1., 1.])
5
>>> arr3 = np.array([[1, 2], [3, 4]])
6
>>> arr4 = np.array([[5, 6], [7, 8]])
7
>>> np.concatenate((arr3, arr4))
8
array([[1, 2],
9
       [3, 4],
10
       [5, 6],
11
       [7, 8]])
12
>>> np.concatenate((arr3, arr4), axis=1) # 可以指定拼接的维度
13
# 在NumPy中，维度（diamension）被称为“轴”（axis），所以上面的语法是`axis=1`*
14
array([[1, 2, 5, 6],
15
       [3, 4, 7, 8]])
16
>>> np.vstack((arr3, arr4)) # 垂直拼接（vertically stack的缩写）
17
array([[1, 2],
18
       [3, 4],
19
       [5, 6],
20
       [7, 8]])
21
>>> np.hstack((arr3, arr4)) # 水平拼接（horizontal stack的缩写）
22
array([[1, 2, 5, 6],
23
       [3, 4, 7, 8]])

切割数组#

切割数组最常用的方式就是用[]来索引，也可以使用np.vsplit()和np.hsplit()

1
>>> arr
2
array([[ 1,  2,  3,  4,  5,  6],
3
       [ 7,  8,  9, 10, 11, 12],
4
       [13, 14, 15, 16, 17, 18],
5
       [19, 20, 21, 22, 23, 24]])
6
>>> np.vsplit(arr, 2) # 横着切，平均切成2份
7
[array([[ 1,  2,  3,  4,  5,  6],
8
       [ 7,  8,  9, 10, 11, 12]]), array([[13, 14, 15, 16, 17, 18],
9
       [19, 20, 21, 22, 23, 24]])]
10
>>> np.hsplit(arr, 3) # 竖着切，平均切成3份
11
[array([[ 1,  2],
12
       [ 7,  8],
13
       [13, 14],
14
       [19, 20]]), array([[ 3,  4],
15
       [ 9, 10],
16
       [15, 16],
17
       [21, 22]]), array([[ 5,  6],
18
       [11, 12],
19
       [17, 18],
20
       [23, 24]])]

数组的形状#

属性	含义
`arr.ndim`	数组的维数
`arr.shape`	数组的形状
`arr.size`	数组的元素个数

1
>>> arr
2
array([[1, 2, 3],
3
       [9, 8, 7]])
4
>>> arr.ndim
5
2
6
>>> arr.shape # arr.shape是一个tuple，表示每一维的容量
7
(2, 3)
8
>>> arr.size # 一共有6个元素，等于arr.shape里每一个数字相乘
9
6

arr.reshape()可以改变数组的形状，我们在前面的例子里已经用到了。

1
>>> arr
2
array([0, 1, 2, 3, 4, 5])
3
>>> arr.reshape(3, 2)
4
array([[0, 1],
5
       [2, 3],
6
       [4, 5]])

使用np.newaixs或np.expand_dims可以给一个数组增加维度。

1
>>> arr = np.array([1, 2, 3, 4, 5, 6])
2
>>> arr.shape
3
(6,)
4
>>> arr1 = arr[:, np.newaxis] # 等价于arr1 = np.expand_dims(arr, axis=1)
5
>>> arr1.shape
6
(6, 1)
7
>>> arr2 = arr[np.newaxis, :] # 等价于arr2 = np.expand_dims(arr, axis=0)
8
>>> arr2.shape
9
(1, 6)
10
>>>

条件筛选#

NumPy里的数组支持按条件筛选出一些元素，如：

1
>>> arr[arr > 5]
2
array([ 6,  7,  8,  9, 10, 11])
3
>>> arr[(arr % 2 == 0) & (arr < 7)] # “且”和“或”要使用“&”和“|”来表示，这是为了防止歧义
4
array([0, 2, 4, 6])

这看上去很神奇，NumPy是怎么做到的呢？让我们输出一下arr > 5

1
>>> arr > 5
2
array([[False, False, False],
3
       [False, False, False],
4
       [ True,  True,  True],
5
       [ True,  True,  True]])

arr > 5不过是个布尔数组，而arr[arr > 5]只是把所有True对应的元素列出来而已。

因此这样操作也是可行的：

1
>>> condition = (arr % 2 == 0) & (arr < 7)
2
>>> arr[condition]
3
array([0, 2, 4, 6]) # 和上面那个效果一样

np.nonzero()可以找到数组里面的非0元素

1
>>> arr = np.array([[0, 0, 1], [2, 0, 0], [1, 0, 1]])
2
>>> np.nonzero(arr)
3
(array([0, 1, 2, 2], dtype=int64), array([2, 0, 0, 2], dtype=int64))

np.nonzero()会返回一个元组，元组的大小等于arr.ndim，元组里面是数组，描述了每一维非零的元素在哪里。

这个形式看起来不是很直观，用zip()处理一下，就可以得到每个非零元素的坐标。

1
>>> list(zip(*np.nonzero(arr)))
2
[(0, 2), (1, 0), (2, 0), (2, 2)]

这里的*是参数解包语法

np.nonzero()也可以用来处理上面提到的布尔数组，因为在Python里，False被看做0，True被看做1。

view和copy#

arr.view()和arr.copy()分别对应浅拷贝和深拷贝，前者类似与C++中的引用，只是一个别名，后者就是创建一个新的数组，只是里面的数据和原数组一致。

view#

1
>>> a = np.ones((3, 3))
2
>>> b = a
3
>>> b[0, 0] = 0 # 改变b的第一个元素
4
>>> b
5
array([[0., 1., 1.],
6
       [1., 1., 1.],
7
       [1., 1., 1.]])
8
>>> a
9
array([[0., 1., 1.],
10
       [1., 1., 1.],
11
       [1., 1., 1.]]) # 结果a也被改变了

出现这个情况是因为NumPy默认使用浅拷贝，从而减少数据的复制，b = a就相当于b = a.view()，提高性能，b = a.view()可以把b变成和a看起来一样的数组，但实际上两个变量还是共享同样的数据，因此改变其中一个，两个都会改变。

要注意的是，切片创建的数组也算view

1
>>> a = ones((3, 3))
2
>>> c = a[:, 0]
3
>>> c += 1
4
>>> c
5
array([2., 2., 2.])
6
>>> a
7
array([[2., 1., 1.],
8
       [2., 1., 1.],
9
       [2., 1., 1.]])

如果要复制一个数组，而不是创建一个引用，就要使用arr.copy()

1
>>> a = np.zeros((3, 3))
2
>>> b = a.copy()
3
>>> b[2] = 3
4
>>> a
5
array([[0., 0., 0.],
6
       [0., 0., 0.],
7
       [0., 0., 0.]])
8
>>> b
9
array([[0., 0., 0.],
10
       [0., 0., 0.],
11
       [3., 3., 3.]])

对数组运算#

广播机制#

对一个数组执行某种基本运算（包括但不限于+、-、*、/、**、%），NumPy会自动地把它变成对数组里每个元素的运算，这是NumPy的“广播”（broadcasting）机制。

对于一元运算符，广播很简单，就是将这个运算应用到每一个数上，如np.exp()、np.sqrt()等都算一元运算符。

对于二元运算符，广播机制的具体规则是这样的：

如果两个数组的维数不同，numpy会在维数小的那一个数组的shape前面添加若干个“1”。如(3, 4) * (1, 2, 3, 4)->(1, 1, 3, 4) * (1, 2, 3, 4)。
然后，NumPy会从前到后比较每一维，设两个数组在这一维的容量分别为 $n$ 、 $m$ ，有三种情况
1. $n=m$ ，则结果的容量也是这个数，如(3, 4) + (3, 4) = (3, 4)
2. $n\neq m$ ，但是 $n$ 和 $m$ 中有一个等于 $1$ ，则NumPy会将等于 $1$ 的这一维自动地对齐另外一个数组，如(5, 1, 4) - (5, 3, 4) -> (5, 3, 4) - (5, 3, 4)
3. $n\neq m$ ，且没有一个等于 $0$ ，程序将会报错。
执行2直到数组中的元素可以直接计算，比如对于+、-、*、/等数值类型的运算符，会广播到最后一维，再对里面存放的数值变量执行两两相加/减/乘/除。对于@（表示矩阵乘法）这种针对二维数组的运算符，会广播直到倒数第二维，再开始两两矩阵乘。

猜猜下面代码输出什么

1
>>> a = np.random.random((3, 5))
2
>>> b = np.random.random((4, 5, 7))
3
>>> c = a @ b
4
>>> c.shape

答案

`(4, 3, 7)` 这是因为

1
   (3, 5) @ (4, 5, 7)
2
-> (1, 3, 5) @ (4, 5, 7)
3
-> (4, 3, 5) @ (4, 5, 7)
4
=  (4, 3, 7)

这里，我引用一些官方文档中的图片来帮助你理解

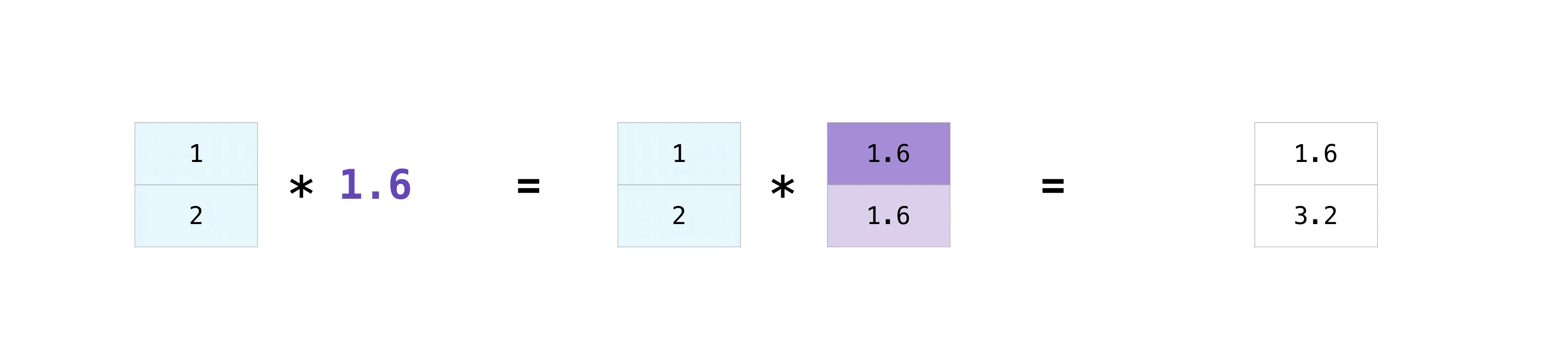
multiply broadcasting

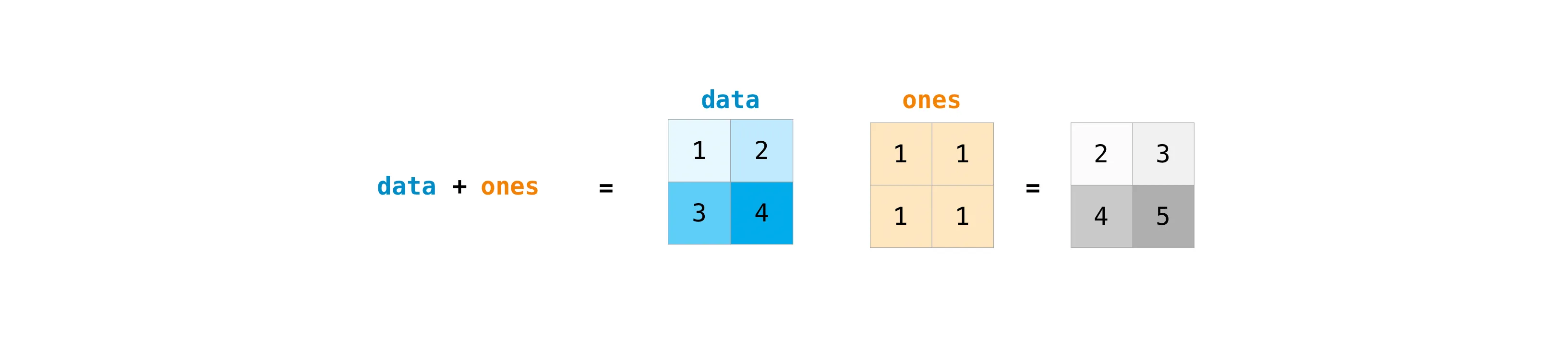
matrix arithmetic

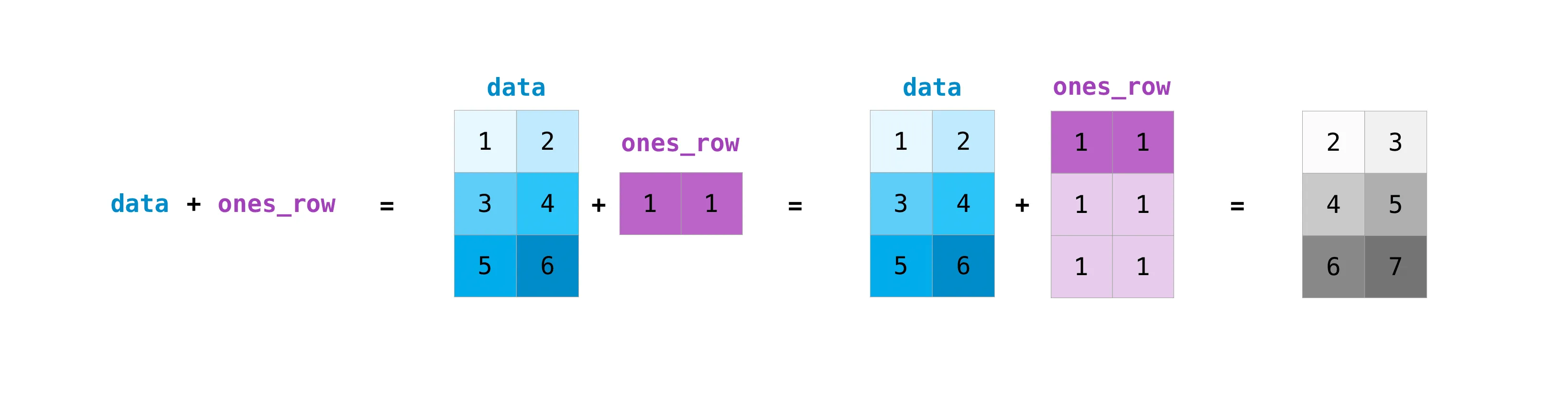
matrix broadcasting

1
>>> a = np.ones(2)
2
>>> a * 2
3
array([2., 2.])
4
>>> a / 3
5
array([0.33333333, 0.33333333])
6
>>> b = np.array([1, 2])
7
>>> b ** 2
8
array([1, 4])
9
>>> a - b
10
array([ 0., -1.])
11
>>> a += 3
12
>>> a
13
array([4., 4.])
14
>>> a * b # 要注意的是这里并不是矩阵乘法，只是单纯将对应元素相乘
15
array([4., 8.])
16
>>> c = np.array([[1, 2], [3, 4]])
17
>>> d = np.array([5, 6])
18
>>> c + d
19
array([[ 6,  8],
20
       [ 8, 10]])

一些运算的示例#

arr.sum()可以对数组求和，arr.max()和arr.min()可以求最大最小值

1
>>> a = np.array([[1, 2], [3, 4]])
2
>>> a.sum()
3
10
4
>>> a.sum(axis=0) # 也可以指定求和某一维
5
array([4, 6])
6
>>> a.sum(axis=1)
7
array([3, 7])
8
>>> a.max()
9
4
10
>>> a.min(axis=1)
11
array([1, 3])

除了np.sum()外，NumPy还提供了很多其他的数学函数，用来替代Python的math库的函数，如np.sqrt()、np.sin()、np.exp()等

获取不同的元素#

np.unique()可以获取不同的元素

1
>>> a = np.array([[0, 0, 1, 2], [1, 2, 0, 4], [0, 0, 1, 2]])
2
>>> np.unique(a)
3
array([0, 1, 2, 4])
4
>>> np.unique(a, return_index=True) # 返回元素的位置，[0, 1, 2, 4]的位置为[0, 2, 3, 7]
5
(array([0, 1, 2, 4]), array([0, 2, 3, 7], dtype=int64))
6
>>> np.unique(a, return_counts=True) # 返回元素的数量，[0, 1, 2, 4]各有[5, 3, 3, 1]个
7
(array([0, 1, 2, 4]), array([5, 3, 3, 1], dtype=int64))
8
>>> np.unique(a, axis=0)  # 指定axis，返回独一无二的行，而不是元素
9
array([[0, 0, 1, 2],
10
       [1, 2, 0, 4]])

反转数组#

用np.flip()

1
>>> arr
2
array([[0, 1, 2],
3
       [3, 4, 5]])
4
>>> np.flip(arr)
5
array([[5, 4, 3],
6
       [2, 1, 0]])
7
>>> np.flip(arr, axis=1)
8
array([[2, 1, 0],
9
       [5, 4, 3]])

压平数组#

arr.flatten()和arr.ravel()都可以压平一个数组，但是前者会创建一个copy，后者不会，因此后者有更高的性能，但是对后者进行修改会影响到原数组。

1
>>> a = np.array([[1, 1, 4], [5, 1, 4]])
2
>>> b = a.flatten()
3
>>> c = a.ravel()
4
>>> a
5
array([[1, 1, 4],
6
       [5, 1, 4]])
7
>>> b
8
array([1, 1, 4, 5, 1, 4])
9
>>> c
10
array([1, 1, 4, 5, 1, 4])
11
>>> b[2] = 0
12
>>> a
13
array([[1, 1, 4],
14
       [5, 1, 4]])
15
>>> c[2] = 0
16
>>> a
17
array([[1, 1, 0],
18
       [5, 1, 4]])

保存和读取NumPy数组#

有多种方法保存NumPy数组

函数	含义	后缀名	读取
`np.save()`	保存单个数组	`.npy`	`np.load()`
`np.savez()`	在一个文件中保存多个数组	`.npz`	`np.load()`
`np.savez_compressed()`	和上一个一样，但是有压缩，生成的文件体积更小	`.npz`	`np.load()`
`np.savetxt()`	用文本形式保存，便于共享，但速度和体积都不如上面三个	`.csv`或`.txt`	`np.loadtxt()`

1
>>> a
2
array([0.08451327, 0.75102915, 0.94578432])
3
>>> b
4
array([[0.80930188, 0.38539336],
5
       [0.5628236 , 0.22558801],
6
       [0.25427619, 0.52475443]])
7
>>> np.save('file1', a) # 保存到文件“file1.npy”
8
>>> np.load('file1.npy')
9
array([0.08451327, 0.75102915, 0.94578432])
10
>>> np.savez('file2', apple=a, banana=b) # 保存多个数组，并添加标识“apple”和“banana”
11
>>> data = np.load('file2.npz') # 保存到文件“file2.npz”
12
>>> data['apple']
13
array([0.08451327, 0.75102915, 0.94578432])
14
>>> data['banana']
15
array([[0.80930188, 0.38539336],
16
       [0.5628236 , 0.22558801],
17
       [0.25427619, 0.52475443]])
18
>>> np.savetxt('file3.csv', a) # 保存到文件“file3.csv”
19
>>> np.loadtxt('file3.csv')
20
array([0.08451327, 0.75102915, 0.94578432])

使用NumPy进行线性代数计算#

用NumPy处理线性代数的矩阵可以使用NumPy中的矩阵库numpy.matlib，这个库里面有所有numpy命名空间里面的函数，但是换成了矩阵版本的。

1
>>> import numpy as np
2
>>> import numpy.matlib
3
>>> arr = np.ones(3)
4
>>> arr
5
array([1., 1., 1.])
6
>>> arr.shape
7
>>> arr.shape
8
(3,)
9
>>> mat = np.matlib.ones(3)
10
>>> mat
11
matrix([[1., 1., 1.]])
12
>>> mat.shape
13
(1, 3)

从这里我们可以看出ndarray和matrix的主要区别，ndarray不区分行向量和列向量（对多维数组进行切片操作会变成一维数组），但是matrix区分（对矩阵切片仍然是矩阵）。用(1, n)和(n, 1)和代表行向量和列向量。

使用np.asarray()和np.asmatrix()可以将二者互相转换。

官方文档里推荐使用np.matlib.mat()代替np.matlib.matrix()创建矩阵，因为这样可以不拷贝原数组，提高效率。

矩阵转置#

矩阵转置使用arr.T

1
>>> mat = np.matlib.mat([[0, 1, 2], [3, 4, 5]])
2
>>> mat
3
matrix([[0, 1, 2],
4
        [3, 4, 5]])
5
>>> mat.T
6
matrix([[0, 3],
7
        [1, 4],
8
        [2, 5]])

矩阵乘法#

NumPy为矩阵乘法提供了专门的运算符@，相当于np.matmul(a, b)

1
>>> mat
2
matrix([[0, 1, 2],
3
        [3, 4, 5]])
4
>>> mat.T
5
matrix([[0, 3],
6
        [1, 4],
7
        [2, 5]])
8
>>> a = np.matlib.mat([[1, 2], [3, 4]])
9
>>> b = np.matlib.mat([[5, 6], [7, 8]])
10
>>> a @ b
11
matrix([[19, 22],
12
        [43, 50]])

矩阵求逆#

NumPy提供了np.linalg.inv()函数来计算矩阵的逆。

1
>>> c = np.matlib.mat([[2, 0], [1, 3]])
2
>>> inv_c = np.linalg.inv(c)
3
>>> inv_c
4
matrix([[ 0.5       ,  0.        ],
5
        [-0.16666667,  0.33333333]])

特征值和特征向量#

NumPy还提供了计算矩阵特征值和特征向量的函数 np.linalg.eig()。

1
>>> d = np.matlib.mat([[4, 2], [1, 3]])
2
>>> eigvals, eigvecs = np.linalg.eig(d)
3
>>> eigvals
4
array([5., 2.])
5
>>> eigvecs
6
matrix([[ 0.89442719, -0.70710678],
7
        [ 0.4472136 ,  0.70710678]])

eigvals 是矩阵 d 的特征值，eigvecs 是对应的特征向量。

奇异值分解#

奇异值分解（SVD）可以使用 np.linalg.svd() 函数进行计算。

1
>>> e = np.matlib.mat([[1, 2], [3, 4], [5, 6]])
2
>>> U, S, Vt = np.linalg.svd(e)
3
>>> U
4
matrix([[-0.2298477 ,  0.88346102,  0.40824829],
5
        [-0.52474482,  0.24078249, -0.81649658],
6
        [-0.81964194, -0.40189603,  0.40824829]])
7
>>> S
8
array([9.52551809, 0.51430058])
9
>>> Vt
10
matrix([[-0.61962948, -0.78489445],
11
        [-0.78489445,  0.61962948]])

这里，U 是左奇异矩阵，S 是奇异值数组，Vt 是右奇异矩阵。

更多线性代数计算请看官方文档。

参考链接#

官方文档